Comment les modèles de fondation tabulaires pourraient redéfinir les outils de la data science ?

N’oublions pas les données tabulaires !

Pour l’essentiel, les progrès récents de l’IA – qu’il s’agisse de systèmes capables d’entretenir une conversation cohérente ou de générer des séquences vidéo réalistes – sont à mettre au crédit des réseaux de neurones (RN) artificiels. Ces prouesses ont été rendues possibles par des avancées algorithmiques et des innovations d’architecture développées au cours des quinze dernières années et, plus récemment, par la construction d’infrastructures de calcul permettant d’entraîner ces RN sur des corpus de données à l’échelle d’Internet.

L’atout principal de cette forme de machine learning, communément désignée par le terme deep learning, réside dans sa capacité à construire des représentations de données complexes – comme les images ou les textes – sans qu’aucune modélisation humaine ne soit nécessaire. Les méthodes de DL constituent à ce titre une avancée décisive dans l’extension des approches statistiques, initialement conçues pour analyser des données structurées en tables, comme celles que l’on trouve dans les feuilles de calcul ou celles hébergées dans les bases de données relationnelles.

Considérant, d’une part, l’efficacité inouïe du deep learning sur des données complexes et, d’autre part, l’immense valeur économique des données tabulaires, qui constituent l’essentiel du patrimoine informationnel de nombreuses organisations, se pose naturellement la question de l’application des outils du deep learning à ces données structurées. Qui peut le plus peut le moins, est-on en droit de penser.

Paradoxalement, le deep learning s’avère a priori plutôt démuni face aux données tabulaires [8]. Pour le comprendre, rappelons que son efficacité tient à sa capacité à identifier des motifs (patterns) grammaticaux, sémantiques ou visuels à partir d’immenses volumes de données. Ainsi, très schématiquement, le sens d’un mot émerge de la cohérence des contextes dans lesquels il apparaît. De même, un élément visuel est identifiable parce qu’il est récurrent dans un grand nombre d’images. Dit autrement, c’est la cohérence propre à ces types de données complexes qui permet au deep learning d’opérer un transfert de connaissances entre différentes images ou différents textes.

Il en va très différemment, en revanche, des éléments d’une table, où chaque ligne représente généralement l’observation d’une relation entre plusieurs variables. Pensons, par exemple, au poids d’un individu en fonction de sa taille, de son âge et de son genre, ou encore à la consommation électrique d’un logement (en kWh) en fonction de sa superficie, de son niveau d’isolation et de la température extérieure. Le point crucial à noter est que la valeur d’une cellule n’a de sens que dans le contexte spécifique de la table où elle se trouve. Ainsi, un même chiffre peut représenter le poids (en kilos) d’un individu dans une table et la superficie (en mètres carrés) d’un studio dans une autre. Dans ces conditions, il est difficile d’imaginer comment un modèle prédictif pourrait transférer la connaissance acquise sur une table pour la réutiliser sur une autre !

Les structures tabulaires sont donc extrêmement hétérogènes, et il en existe en réalité une infinité pour décrire toute la diversité du réel, qu’il s’agisse de transactions financières, de structures de galaxies ou encore de la disparité des revenus dans une agglomération.

Cette diversité des modèles tabulaires a toutefois un prix car chaque jeu de données tabulaires requiert son propre modèle prédictif, qui n’est pas réutilisable.

Pour traiter ce type de données, les data scientists privilégient le plus souvent une catégorie de modèles prédictifs fondés sur les arbres de décision [7]. Peu importe ici leur nature précise : il suffit de savoir qu’ils offrent d’excellentes performances en termes de rapidité de calcul, avec des temps de latence souvent inférieurs à la milliseconde. Hélas, comme pour tout algorithme de machine learning classique, chaque nouvelle table requiert un nouvel entraînement du modèle, qui peut se chiffrer en heures ! À cela s’ajoutent un manque de fiabilité dans l’estimation de l’incertitude des prédictions, des difficultés d’interprétation et une combinaison délicate avec des données non structurées, sur lesquelles les réseaux de neurones excellent.

On conçoit dès lors tout l’intérêt qu’il y aurait à construire des modèles prédictifs universels, un peu à l’image des LLM, qui, une fois préentraînés, seraient utilisables tels quels, sans entraînement supplémentaire ni fine-tuning, sur tout type de données tabulaires. Formulé ainsi, le projet peut paraître audacieux, voire carrément irréaliste. C’est pourtant ce à quoi parviennent, avec un succès inespéré, les modèles de fondation tabulaires (TFM) développés par plusieurs laboratoires [2–4] depuis un peu plus d’un an.

Les sections qui suivent présentent quelques-unes des innovations sur lesquelles reposent ces TFM et les comparent aux techniques existantes. Son but principal est cependant d’éveiller la curiosité du lecteur pour une avancée qui promet de redéfinir à court terme les outils de la data science.

Ce que nous ont appris les LLM

Rappelons, en schématisant à l’extrême, qu’un LLM est un modèle de machine learning entraîné à prédire le mot suivant dans une séquence de texte. L’une des caractéristiques les plus remarquables de ces systèmes est que, une fois entraînés sur d’immenses corpus, ils se révèlent capables de résoudre une grande diversité de tâches linguistiques ou logiques pour lesquelles ils n’ont pas été entraînés explicitement. L’une des manifestations les plus frappantes de cette aptitude est leur capacité à résoudre des problèmes à partir d’une simple liste d’exemples de « questions-réponses ». Ainsi, pour une tâche de traduction, il suffira de donner au LLM quelques exemples dans un prompt.

On désigne ce comportement des LLM par le terme in-context learning (ICL). L’apprentissage et la prédiction s’effectuent ici dans la foulée, sans qu’aucun entraînement supplémentaire du modèle ne soit nécessaire. Ce phénomène, presque miraculeux et initialement inattendu, est naturellement au cœur des prouesses de l’IA générative. Récemment, plusieurs équipes de recherche ont proposé d’adapter ce mécanisme d’ICL, presque miraculeux, pour construire des modèles de fondation tabulaires (TFM), appelés à jouer pour les données tabulaires un rôle analogue à celui des LLM pour les textes.

Sur le plan conceptuel, la construction d’un TFM reste relativement simple. Dans un premier temps, il s’agit de générer une (très) grande quantité de données tabulaires synthétiques, présentant des structures variées et des tailles différentes, tant par le nombre de lignes (observations) que par celui de colonnes (features ou covariates). Dans un second temps, on entraîne un modèle unique – le modèle de fondation proprement dit – à prédire, pour chacune de ces tables, une colonne en fonction de toutes les autres. Les données d’une table jouent ainsi le rôle d’un contexte prédictif, analogue aux exemples d’un prompt utilisé par un LLM en mode ICL.

L’utilisation de données synthétiques présente plusieurs avantages. Le premier est d’éviter les problèmes de droits d’auteur ou d’atteinte à la vie privée qui font peser un risque juridique sur l’entraînement des LLM. Le second est de permettre l’injection d’une connaissance préalable (un biais inductif) dans cet immense corpus. Un choix particulièrement efficace consiste à générer ces données tabulaires à l’aide de modèles causaux. Sans entrer dans des détails trop techniques, disons simplement que ces modèles simulent les mécanismes susceptibles de produire toute la diversité de données que l’on observe dans le monde réel (physique, économique, etc.). Dans les TFM récents comme TabPFN-v2 ou TabICL [3,4], plusieurs dizaines de millions de tables ont ainsi été générées à partir d’autant de modèles causaux. Ceux-ci sont construits « au hasard », tout en privilégiant les modèles les plus simples, conformément au principe du Rasoir d’Occam, qui commande de favoriser les explications les plus sobres compatibles avec les observations.

Les TFM sont tous implémentés à l’aide des réseaux de neurones. Les architectures varient d’une implémentation de TFM à l’autre, mais toutes intègrent un ou plusieurs modules de type Transformer. Ce choix s’explique, de façon très schématique, par le fait qu’un Transformer met en œuvre un mécanisme dit d’« attention », qui permet de contextualiser chaque bribe d’information. De même qu’il situe un mot dans son contexte au sein d’un texte pour en faire émerger le sens, un mécanisme d’attention approprié saura contextualiser la valeur d’une cellule dans une table. Pour approfondir ce sujet fascinant mais un peu technique le lecteur curieux pourra se reporter aux références [2–4].

Les figures 2 et 3 comparent les phases d’entraînement et de prédiction des modèles classiques avec celles des TFM. Les modèles traditionnels, comme XGBoost [7], doivent être réentraînés pour chaque nouvelle table. Ils apprennent alors à prédire une cible y = f(x) à partir des features x. Leur entraînement prend typiquement plusieurs heures, tandis que leurs prédictions sont presque instantanées.

Les TFM, quant à eux, nécessitent un préentraînement initial plus coûteux, de l’ordre de quelques dizaines de jours-GPU en principe pris en charge par le fournisseur mais qui reste accessible à de nombreuses organisations (contrairement aux LLM). Une fois ce préentraînement effectué, l’apprentissage en mode ICL et la prédiction se confondent : la table D pour laquelle on souhaite faire des prédictions joue fait office de contexte pour les données de test x. Un TFM prédit ainsi une cible y = f(x; D), où la structure de données D joue un rôle analogue à celui d’une liste d’exemples fournie dans le prompt d’un LLM.

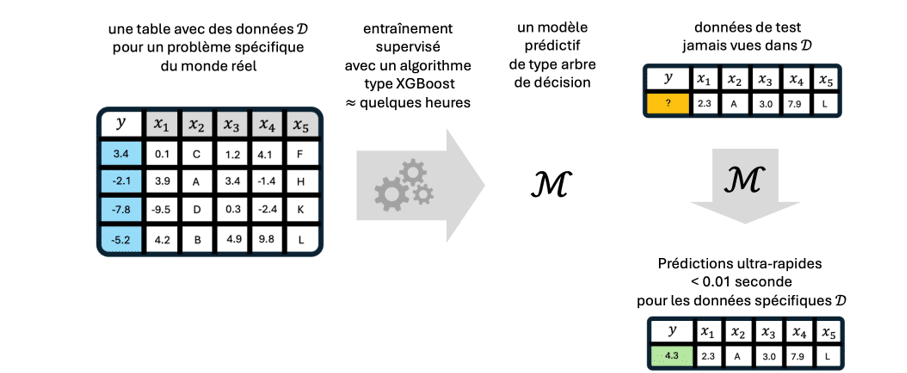
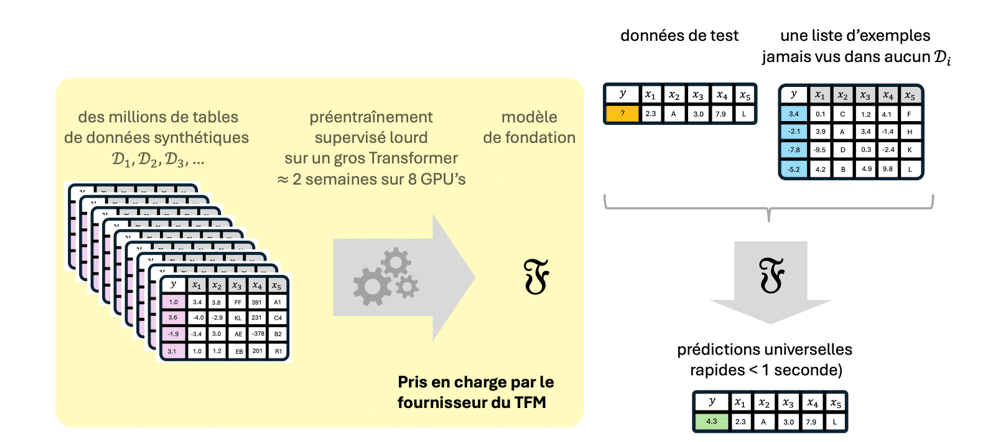
Résumons d’une phrase la discussion précédente :

Les TFM sont conçus pour apprendre à la volée un modèle prédictif pour des données tabulaires sans nécessiter aucun entraînement.

Des performances qui décoiffent

Quelques chiffres

Le tableau ci-dessous donne quelques ordres de grandeur concernant le coût du préentraînement d’un TFM, le temps d’apprentissage en mode ICL pour une nouvelle table, les temps d’inférence ainsi que les tailles maximales de tables prises en charge par trois modèles prédictifs : TabPFN-v2, un TFM développé chez PriorLabs dans l’équipe de Frank Hutter ; TabICL, un TFM développé à l’INRIA dans l’équipe de Gaël Varoquaux[1] ; et enfin XGBoost, un algorithme classique généralement considéré comme l’un des plus performants sur les données tabulaires.

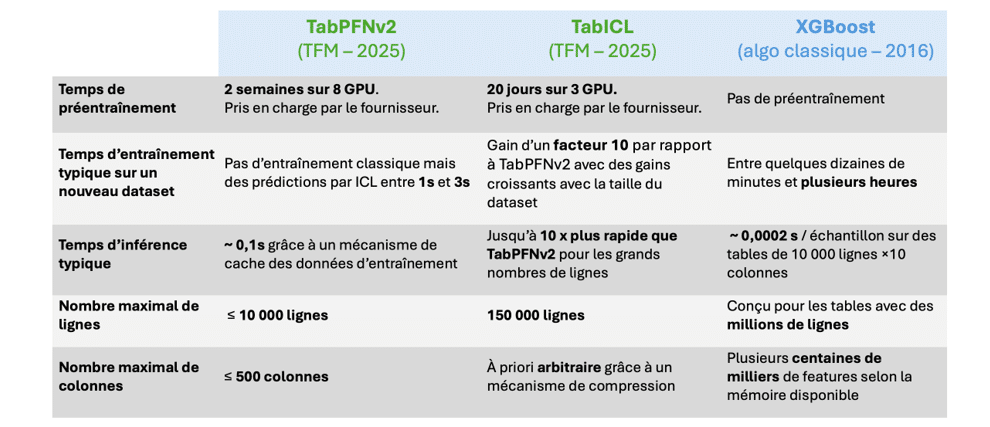
Ces chiffres doivent être considérés comme des ordres de grandeur. Par ailleurs ils évoluent rapidement avec les progrès des différentes implémentations. Pour une analyse détaillée, on pourra se reporter aux articles originaux [2–4].

Au-delà de ces aspects quantitatifs, les TFM présentent d’autres atouts importants par rapport aux approches usuelles. Voici les principaux.

Les TFN sont bien calibrés

Un point faible des modèles classiques est leur mauvaise calibration, c’est-à-dire que les probabilités qu’ils attribuent à leurs prédictions ne correspondent pas aux fréquences observées. Les TFM, en revanche, sont bien calibrés par construction, pour des raisons qu’il serait trop long de détailler ici, mais qui tiennent à leur caractère implicitement bayésien [1].

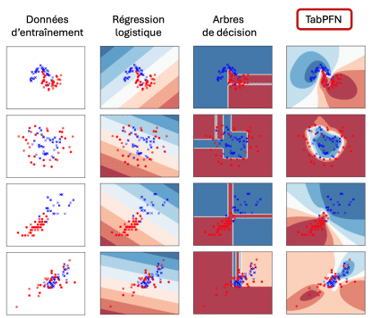
La figure 5 compare niveau de confiance prédits par les TFM avec celles de modèles classiques tels que la régression logistique ou les arbres de décision. Ces derniers affichent des niveaux de confiance largement excessifs dans des régions pourtant dépourvues de données, et présentent en outre des artefacts linéaires sans lien avec les observations. À l’inverse, les prédictions de TabPFN apparaissent nettement mieux calibrées.

Les TFN sont robustes

Les données synthétiques utilisées pour préentraîner les TFM (des millions de structures causales) peuvent être choisies de manière judicieuse afin de les rendre extrêmement robustes aux valeurs aberrantes, aux données manquantes ou aux features non informatives. En effet, en exposant le modèle dès l’entraînement à de tels cas de figure, on l’habitue à les reconnaître et à les traiter correctement, comme l’illustre la figure 6.

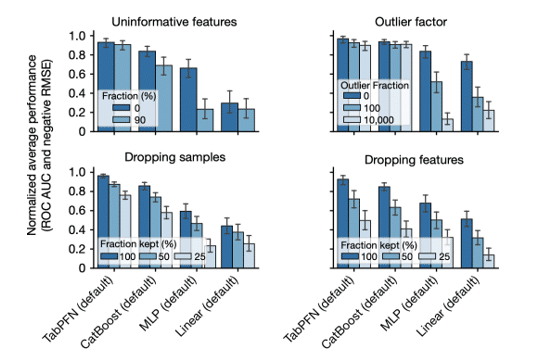
Les TFN demandent peu d’ajustements d’hyperparamètres

Une dernière bonne nouvelle concernant les TFM est qu’ils ne nécessitent que très peu d’ajustements d’hyperparamètres. De plus, ils se révèlent souvent plus performants dans leur configuration par défaut que les meilleurs algorithmes classiques longuement optimisés comme l’illustre la figure 7.

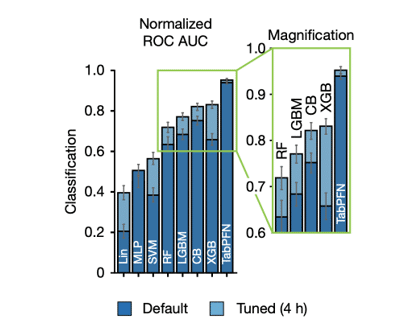
Pour conclure mentionnons que la recherche sur les TFN laisse penser qu’ils offrent aussi des perspectives prometteuses en terme d’explicabilité [3], de prédiction équitables (fairness) [5] et d’inférence causale [6].

A chaque équipe de R&D sa sauce secrète !

On l’aura compris, les TFM ne promettent rien de moins que de chambouler, dans un avenir proche, les méthodes et les outils de la data science. Pour autant qu’on puisse le prévoir, celle-ci pourrait progressivement délaisser l’approche centrée sur la conception et l’optimisation de modèles prédictifs au profit d’une démarche plus data-centric. Un data scientist en entreprise aura ainsi pour mission, non plus de construire un modèle prédictif, mais plutôt de constituer un jeu de données représentatives destiné à conditionner un TFN préalablement préentraîné.

Il est également envisageable que de nouvelles méthodes d’analyse exploratoire voient le jour, portées par la rapidité avec laquelle les TFM permettent aujourd’hui de construire des modèles prédictifs sur de nouvelles données et par leur applicabilité aux séries temporelles [9].

Ces perspectives n’ont évidemment pas échappé à de nombreuses startups et laboratoires académiques, qui rivalisent désormais pour proposer des TFM toujours plus performants. Les deux ingrédients principaux de cette compétition – la « sauce » plus ou moins secrète de chaque solution – sont, d’une part, la stratégie de génération des données synthétiques et, d’autre part, l’architecture du réseau de neurones qui implémente le TFM.

Voici deux points d’entrée possibles pour découvrir et explorer ces nouveaux outils :

1. TabPFN (Prior Labs) Librairie locale en Python : tabpfn défini des classes compatibles scikit-learn (fit/predict). Accès libre (licence de type Apache 2.0 avec exigence d’attribution).
2. TabICL (Inria Soda) Librairie locale en Python : tabicl (préentraînement sur des jeux tabulaires synthétiques ; classification, ICL). Accès libre (BSD-3-Clause).

Bonne exploration à tous !

 

Références

1.       Müller, S., Hollmann, N., Arango, S. P., Grabocka, J., & Hutter, F. (2021). Transformers can do bayesian inference. arXiv preprint arXiv:2112.10510, publié pour ICLR 2021.

2.       Hollmann, N., Müller, S., Eggensperger, K., & Hutter, F. (2022). Tabpfn: A transformer that solves small tabular classification problems in a second. arXiv preprint arXiv:2207.01848, publié pour NeurIPS 2022.

3.       Hollmann, N., Müller, S., Purucker, L., Krishnakumar, A., Körfer, M., Hoo, S. B., … & Hutter, F. (2025). Accurate predictions on small data with a tabular foundation model. Nature, 637(8045), 319-326.

4.       Qu, J., Holzmmüller, D., Varoquaux, G., & Morvan, M. L. (2025). TabICL: A tabular foundation model for in-context learning on large data. arXiv preprint arXiv:2502.05564, publié pour ICML 2025.

5.       Robertson, J., Hollmann, N., Awad, N., & Hutter, F. (2024). FairPFN: Transformers can do counterfactual fairness. arXiv preprint arXiv:2407.05732, publié pour ICML 2025.

6.       Ma, Y., Frauen, D., Javurek, E., & Feuerriegel, S. (2025). Foundation Models for Causal Inference via Prior-Data Fitted Networks. arXiv preprint arXiv:2506.10914.

7.       Chen, T., & Guestrin, C. (2016, August). Xgboost: A scalable tree boosting system. In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining (pp. 785-794).

8.       Grinsztajn, L., Oyallon, E., & Varoquaux, G. (2022). Why do tree-based models still outperform deep learning on typical tabular data? Advances in neural information processing systems, 35, 507-520.

9.       Liang, Y., Wen, H., Nie, Y., Jiang, Y., Jin, M., Song, D., … & Wen, Q. (2024, August). Foundation models for time series analysis: A tutorial and survey. In Proceedings of the 30th ACM SIGKDD conference on knowledge discovery and data mining (pp. 6555-6565).

 

[1] Gaël Varoquaux is one of the original architects of the Scikit-learn API. He is also co-founder and scientific advisor at the startup Probabl.