Les LLM comprennent-ils ce qu’est une chaise ?

Cherchons la faille !

Les LLM ont-ils acquis une forme de bon sens à force d’avoir lu tous les livres ? Comprennent-ils le monde au moyen de représentations et de concepts similaires aux nôtres ? Tentons une rapide mise à l’épreuve de Gemini et ChatGPT avec cette question simple mais taquine :

Question : J’ai fait sécher 12 serviettes en 30 minutes en les mettant au soleil sur une grande pelouse. Combien de temps me faudra-t-il pour en sécher 18 ?

Voici les réponses :

• Gemini : Il est difficile de donner une réponse exacte […] cependant, on peut faire une estimation approximative. Si vous avez séché 12 serviettes en 30 minutes dans des conditions données, on pourrait penser qu’il vous faudrait environ 45 minutes pour sécher 18 serviettes (1,5 fois plus de serviettes, donc 1,5 fois plus de temps) […].
• ChatGPT : Le temps nécessaire pour sécher les serviettes dépend de la quantité de soleil et de la superficie disponible, et non du nombre de serviettes, à condition qu’il y ait assez d’espace pour toutes les étendre en même temps. Donc, si vous avez pu sécher 12 serviettes en 30 minutes dans ces conditions, vous pourrez sécher 18 serviettes en 30 minutes également, tant que les conditions restent les mêmes et que vous avez suffisamment d’espace pour les étendre.

Victoire indiscutable de ChatGPT sur ce coup mais, sur d’autres questions du même type, rien ne garantit que celui-ci soit infaillible. Ce genre d’aberrations jette évidemment une lumière crue sur la capacité des LLM à vraiment comprendre le monde et sur la confiance qu’on peut leur accorder.

Des propriétés émergentes et imprévues

Au cœur de l’intelligence des réseaux de neurones (RN) on trouve l’idée de généralisation. Elle caractérise en fait toute l’approche de l’IA par le machine learning (ML). En termes simples, c’est l’idée qu’un modèle est réputé « intelligent » dès lors qu’il est capable de faire des prédictions sur des données qu’il n’a jamais vues. Ainsi, un système de classification d’images de chiens et de chats est-il « intelligent » s’il identifie correctement des individus qu’il n’a jamais vus. La situation est nettement plus obscure en revanche pour les LLM. Obscure, mais également fascinante car, entraînés à prédire le mot suivant dans une suite de mots et utilisés en mode autorégressif, ils démontrent grâce à cette martingale des aptitudes cognitives à la fois inattendues et très utiles. Même s’ils sont sujets à des aberrations un peu ridicules, comme nous venons de le voir, ils se montrent néanmoins capables de répondre à des questions ouvertes, de raisonner logiquement, d’apprendre à partir d’un contexte ou de générer du code informatique accompagné d’explications discursives [2]. Autant de tâches sur lesquelles ils n’ont pas été explicitement entraînés.

Il existe une théorie classique (la théorie PAC de l’apprentissage statistique [1,3]) qui vise précisément à comprendre dans quelles conditions apparaît le phénomène de généralisation. Bien qu’il ne puisse être question d’entrer ici dans les arcanes mathématiques de ce sujet, on peut cependant formuler intuitivement l’une de ces conditions. Un modèle de ML « généralise » pour autant que les données utilisées pour l’entraîner soient statistiquement similaires à celles des données auxquelles on l’applique. Le cas des LLM est remarquable en ce sens qu’ils semblent capables de généralisations mystérieuses et bien plus vastes que celles que couvre la théorie PAC. Non seulement ils généralisent sur des données qu’ils n’ont pas vues mais sur des tâches dont ils n’ont pas vu d’exemples explicites ! On parle parfois de généralisation Out Of Distribution (OOD) pour décrire cette situation. À ce jour nul ne comprend au juste comment se produit ce petit miracle. On se contente de l’utiliser à toutes fins utiles^1.

Les praticiens en sont par conséquent réduits à mettre en œuvre les LLM de manière purement empirique, sans qu’aucune théorie ne vienne ni à garantir, ni à étayer leurs capacités de généralisation ! L’expérience montre cependant que les LLM acquièrent des capacités cognitives que même les spécialistes de la discipline n’avaient pas anticipé lorsqu’on augmente au-delà d’un certain seuil, et dans des proportions judicieuses², la quantité de données, la puissance de calcul investie à l’entraînement et le nombre de paramètres. On les qualifie pour cette raison de propriétés émergentes.
Sont-elles la signature de l’apparition de représentations internes qui correspondent à une appréhension du réel alignée sur la nôtre, ce qu’on appelle communément le bon sens ? À défaut de comprendre l’origine exacte de ces propriétés, pourrait-on a minima démontrer leur existence de manière irréfutable ? Se pourrait-il au contraire que nous soyons bernés par des systèmes dépourvus d’intelligence réelle mais capables de régurgiter contextuellement l’intégralité du savoir humain ? La suite de cet article essaie d’apporter quelques modestes éléments de réponse à ces questions.

Les enjeux pratiques de ces sujets sont importants à plusieurs titres. D’une part l’émergence de nouvelles capacités cognitives accréditerait l’idée selon laquelle les LLM constituent un des ingrédients nécessaires dans la quête de l’IAG (intelligence artificielle générale). Parallèlement, leur imprévisibilité pose également des questions de sécurité inédites. Que l’on songe par exemple à une erreur de traduction d’une prescription médicale qui serait imputable à une erreur de compréhension d’une situation clinique. Enfin, pour envisager un partenariat fécond et maîtrisé entre les LLM et les humains, il semble indispensable que nous puissions avoir avec eux un dialogue qui s’articule autour de représentations communes et intelligibles par nous-mêmes.

Performance ne vaut pas compréhension

L’un des premiers tests conçus pour évaluer le bon sens et la capacité de compréhension d’une IA a été proposé par le mathématicien Alan Turing dans les années 1950 qui l’a baptisé « The imitation game ». Dans ce scénario bien connu, une IA est mise à l’épreuve au moyen d’un dialogue textuel avec un humain dont elle est physiquement masquée. Si l’IA parvient à maintenir un dialogue cohérent sur la durée sans que l’humain ne parvienne à déceler la nature artificielle de son interlocuteur on considère que le système « pense », qu’il « comprend » et qu’il est « intelligent ». Ce test est aujourd’hui largement considéré comme caduc par les experts en IA car il néglige la propension des humains à se laisser berner trop facilement, voire à vouloir délibérément être bernés ! Pris au pied de la lettre, ce test serait probablement passé haut la main aujourd’hui par une version débridée de GPT-4 [2].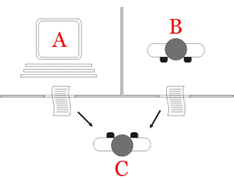

Figure 1 : L’ « Imitation Game » plus connu comme le « test de Turing »

 

D’autres tests, plus rigoureux et moins subjectifs, ont par la suite été imaginés par les chercheurs parmi lesquels les schémas de Winograd qui sont largement reconnus comme un bon moyen d’évaluer le niveau de compréhension d’une IA. Il s’agit de couples de phrases dont le sens bascule par la substitution d’un seul mot. En voici deux exemples :

 

Schéma de Winograd A

Phrase 1 : J’ai versé l’eau de la bouteille dans la tasse jusqu’à ce qu’elle soit pleine.

Question : Qu’est ce qui est plein, la bouteille ou la tasse ?

Phrase 2 : J’ai versé l’eau de la bouteille dans la tasse jusqu’à ce qu’elle soit vide.

Question : Qu’est ce qui est vide, la bouteille ou la tasse ?

 

Schéma de Winograd B

Phrase 1 : La voiture de sport a dépassé la camionnette postale car elle était plus rapide.

Question : Qui est la plus rapide, la voiture de sport ou la camionnette ?

Phrase 2 : La voiture de sport a dépassé la camionnette postale car elle était plus lente.

Question : Qui est la plus lente, la voiture de sport ou la camionnette ?

 

L’idée communément admise est qu’une réponse correcte attestera qu’une IA possède une forme rudimentaire de bon sens.

En 2016 le taux de réponses correctes à ce type de challenge avoisinait 54% pour les meilleurs systèmes. En d’autres termes il était proche d’une réponse donnée au hasard ! Ce score est à comparer à celui des humains qui est proche de 95%. Les plus gros LLM parviennent aujourd’hui à des scores de 97% ! A-t-on pour autant la certitude que ces systèmes ont acquis une réelle compréhension du monde ? Hélas non, et ceci pour plusieurs raisons.

La première est qu’il faut s’assurer que les tests soient « Google-proof » c’est-à-dire que le système n’ait pas simplement appris la réponse lors de l’entraînement. Un moyen simple pour se prémunir de ce risque consiste par exemple à reformuler les questions.

Un problème plus délicat tient au fait qu’il est très difficile d’exclure la possibilité qu’un gros LLM parvienne à exploiter de subtiles corrélations entre les termes d’une question pour y répondre correctement sans pour autant avoir réellement compris la situation qu’elle évoque. Dans le schéma B par exemple, il est possible qu’un LLM établisse une corrélation entre « voiture de sport » et « rapide » sans effectuer aucun raisonnement basé sur une compréhension de ce que « dépasser un véhicule » signifie !

Les schémas de Winograd ont été régulièrement perfectionnés avec des jeux de données comme WinoGrande qui tentent d’éviter ce genre de piège statistique. Mais, à ce jour, il n’y a pas de consensus dans la communauté scientifique pour savoir si ces tests attestent d’une compréhension comparable à celle des humains.

Le doute subsiste essentiellement car il manque aux LLM tout un pan de savoir non-linguistique qui relève de l’expérience sensorielle^3., comme la perception du temps et de l’espace, dont ils sont dépourvus. On parle parfois à ce titre de matière noire de l’IA^4.. Les choses pourraient cependant évoluer prochainement avec l’avènement d’une nouvelle génération de modèles multimodaux, alimentés par des sons, des images et des vidéos, pour lesquels il faudra concevoir de nouveaux tests.

Quelques indices de compréhension à prendre au sérieux

Une approche rigoureuse de la question évoquée dans le titre de cet article demanderait de définir précisément ce que l’on entend par « comprendre ». Nous nous contenterons plus modestement de décrire quelques indices expérimentaux qui suggèrent prudemment qu’il se passe « quelque chose » dans les LLM qui ressemble à une forme de compréhension et que les LLM ne se laissent donc pas réduire à de simples perroquets stochastiques.

Les régularités linguistiques dans les embeddings

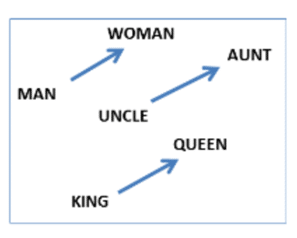
Figure 2 : la relation masculin féminin traduite par une translation dans l’espace de représentations.

 

La première étape de l’encodage sémantique d’un texte par un LLM consiste à encoder le sens de mots isolés dans un espace de représentations par des vecteurs qu’on appelle des « embeddings ». Les chercheurs qui ont conçu les premières versions de ces embedding [10] ont constaté que beaucoup de relations sémantiques se traduisaient par un vecteur de translation spécifique comme l’illustre la figure 3. On peut concevoir cette auto-organisation de l’espace des représentations sémantiques comme un première esquisse, très primitive, de représentation du sens et de compréhension.

Les poèmes et autres licornes de GPT-4

À l’autre extrémité du spectre de complexité, on peut pousser un LLM comme GPT-4 dans ses retranchements pour mettre à l’épreuve ses capacités de compréhension, tout en veillant à éliminer autant que faire se peut tout soupçon de régurgitation triviale de textes vus pendant l’entraînement. À vrai dire créer des tests Google-proof demande un peu d’imagination. Pour relever ce défi des chercheurs ont concocté toute une panoplie de tests [2] dont le caractère intentionnellement farfelu vise précisément à se prémunir de ce risque. Voici deux exemples de compréhension qui semblent assez convaincants.

Dans le premier on demande au LLM de rédiger sous forme de poème avec des rimes une démonstration mathématique de l’existence d’une infinité de nombres premiers. On peut penser que, pour s’acquitter de cette tâche, le modèle devra véritablement comprendre l’essence de la démonstration. Si tel n’était pas le cas il serait en effet incapable de la reformuler en respectant la contrainte linguistique qui est suffisamment extravagante pour que l’on puisse être confiant qu’aucun texte de cet acabit n’ait jamais existé sur internet.

Figure 3 : un poème sur les nombres premiers.

 

Dans le même ordre d’idées les chercheurs ont demandé au LLM de dessiner une licorne à l’aide d’une bibliothèque graphique incorporée au système de traitement de texte scientifique LaTeX. Là encore, la contrainte syntaxique extravagante est conçue pour évaluer la capacité du système à comprendre le concept de licorne (un animal avec quatre pattes, une corne etc.) qui est un préalable à la possibilité de le dessiner sans partir d’une image existante.

Figure 4 : Plusieurs versions de licornes dessinées en LaTeX par GPT-4.

 

Chacun pourra juger de la réussite de ces petits exercices imposés.

Reconnaissance de structures « profondes » en mathématiques

Tester un LLM sur sa capacité à comprendre des concepts mathématiques présente l’avantage de permettre une évaluation plus objective que des considérations sur la qualité d’un poème ou la crédibilité d’une esquisse de licorne. De plus, la restriction aux questions mathématiques ouvre la possibilité d’évaluer différents niveaux de compréhension.

On parle de compréhension superficielle lorsqu’un LLM est capable de résoudre un problème arithmétique en tirant parti d’un prompt qui énumère plusieurs exemples rédigés avec une même syntaxe (compris ici comme la structure d’une chaîne de caractères). Cette compréhension est dite superficielle car elle repose sur la simple identification de schémas syntaxiques pour résoudre un problème de calcul.

À l’inverse, une compréhension profonde demande de reconnaître un concept commun à plusieurs exemples d’un même problème, et ce en dépit de la variabilité des formulations syntaxiques. La figure ci-dessous donne des exemples d’une même question « profonde », le calcul d’une soustraction, avec des formats différents.

Figure 5 : des exemples de soustraction formulés avec des formats différents.

 

Un LLM est-il capable de compréhension profonde ? Pour le savoir, on peut étudier comment varie la précision des réponses (moyennées sur plusieurs problèmes d’arithmétique) selon que l’on utilise un prompt avec des exemples ayant la même structure syntaxique ou, au contraire, un prompt regroupant des exemples ayant des structures syntaxiques différentes mais avec la même structure profonde.

Dans un travail récent (en prépublication) [7] des chercheurs ont évalué ces capacités pour un LLM généraliste (Mistral–7B) ainsi que pour deux LLM spécialisés en mathématiques et en génération de code (Codellama‑7B et LLemma–7B).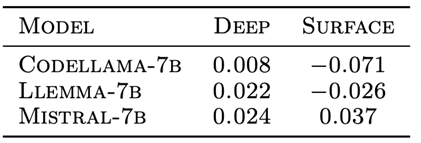

Figure 6 : Variation de la précision des réponses de 3 LLM selon un prompting avec des exemples superficiels ou profonds. Les chiffres indiquent la différence de précision observée par rapport à un prompt standard.

 

Les résultats de la figure 6 semblent indiquer que les LLM spécialisés (Codellama‑7B et LLemma–7B) présentent une amélioration lorsque le prompt contient des exemples profonds. À l’inverse, le LLM généraliste (Mistral–7B) présente une amélioration plus importante lorsque le prompt contient des exemples dont la structure superficielle est la même ce qui suggère que seuls les LLM spécialisés en mathématique bénéficient d’une compréhension profonde de cette discipline. Des résultats, intéressants mais à prendre avec circonspection.

Discontinuités et lois d’échelle dans les LLM

Nous avons évoqué plus haut le caractère discontinu de l’apparition de nouvelles propriétés (in-context learning, raisonnement, etc.) lorsque la complexité des RN dépasse certains seuils. Précisons que la réalité de ces discontinuités ne fait pas l’unanimité parmi les chercheurs. Certains soupçonnent qu’il ne s’agit là que d’artefacts liés au choix de certaines métriques de performance plutôt que de propriétés intrinsèques des LLM [6]. Si l’on admet toutefois que ces discontinuités existent, celles-ci présenteraient alors des analogies remarquables avec un phénomène bien connu des physiciens : les transitions de phases. L’exemple simple est celui d’un métal ferromagnétique qui, lorsqu’on le refroidit au-dessous d’une température critique, présente spontanément une magnétisation. C’est ce que l’on appelle un ordre à longue portée au sens où une fraction macroscopique des atomes s’alignent pour créer un aimant.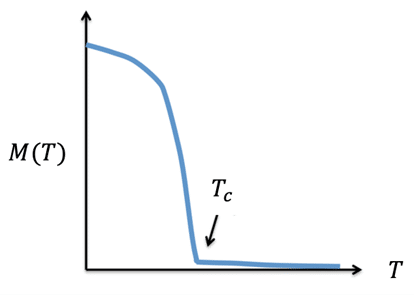

Figure 7 : apparition d’une magnétisation = ordre spontané dans un aimant.

 

Se pourrait-il que les discontinuités observées dans les LLM soient révélatrices de l’apparition de structures ordonnées à l’origine de l’émergence de nouvelles compétences ? C’est possible mais reste à ce stade de la spéculation.

Un autre indice qui pourrait corroborer ce rapprochement est l’observation de lois d’échelle^5.[8] dans les LLM. Celles-ci décrivent comment la fonction de coût d’un LLM évolue avec le nombre de paramètres et avec le volume des données d’entraînement. Les transitions de phase pour lesquelles on observe de telles lois d’échelle en physique sont dites du second ordre et se caractérisent au point critique par des corrélations à longue portée ce qui signifie qu’une intervention locale sur le système a un impact à une distance arbitrairement grande. Intuitivement, la susceptibilité du système devient alors infinie ce qui signale que le système adopte soudain un comportement coopératif à une échelle macroscopique. Faut-il établir un lien avec l’apparition de nouvelles compétences ? La perspective est là encore fascinante mais loin d’être établie à ce jour.

L’intrigant phénomène du « grokking »

Terminons ce tour d’horizon par une découverte récente, fortuite et surprenante qui suggère que dans certaines circonstances un RN découvre brusquement d’authentiques représentations de concepts [4,5]. Nulle spéculation en l’occurrence, tout est vérifiable expérimentalement ! Cette découverte ne concerne pas spécifiquement les LLM mais, plus généralement, tous les modèles de deep learning soumis à un surapprentissage intensif.

Rappelons que l’objectif recherché lorsqu’on entraîne un RN (ou tout autre modèle de ML) est sa capacité de généralisation. La méthode usuelle pour évaluer cette capacité consiste à tracer deux courbes qui représentent respectivement l’évolution de la précision (accuracy) sur les données d’entraînement (train set) et sur des données de validation (test set) en fonction du nombre de passages (epochs) sur les données d’entraînement comme l’illustre la figure 9. Les deux courbes de précision augmentent initialement de concert mais, après un certain laps de temps, la précision sur les données de validation chute, signalant une diminution des capacités de généralisation et un début de surapprentissage. La méthode dite d’early stopping commande alors d’arrêter l’entraînement à cet instant, ce que font tous les data scientists.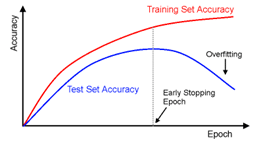

Figure 8 : courbes d’apprentissage sur les données d’entraînement et de validation.

 

Voilà pour la théorie. Pour certains types de données, des chercheurs ont cependant observé un phénomène étonnant et même totalement inattendu illustré dans la figure 10. Celle-ci représente là aussi deux courbes d’apprentissage mais elles sont en violation flagrante avec le comportement précédent !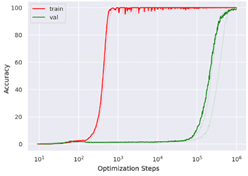

Figure 9 : courbes d’apprentissage lorsque se produite le phénomène du grokking.

 

La courbe rouge, qui représente la précision sur les données d’entraînement, sature rapidement autour d’une précision quasi parfaite de 100% alors que la courbe verte qui est la prédiction pour les données de validation reste proche de à 0%. Mais, contre toute attente, si l’on patiente très, très, très longtemps, en pratique si l’on entraîne le système 1000 fois trop longtemps, la précision sur les données de validation finit elle aussi par atteindre une valeur parfaite ! Le système manifeste une capacité de généralisation tardive mais parfaite ! C’est ce qu’on appelle le phénomène de grokking, un terme d’argot qui signifie quelque chose comme « comprendre profondément et intuitivement ».

Ce phénomène de généralisation tardive a été observé pour des données d’un type particulier que l’on appelle données algorithmiques car elles sont générées artificiellement à partir d’une procédure élémentaire [4,5]. En l’occurrence il s’agissait d’un problème d’arithmétique modulaire. L’addition modulaire, rappelons-le, consiste par exemple à calculer le reste de l’addition de deux nombres modulo un certain entier p. Pour p=12 par exemple on a 7+8 mod 12 = 3. Une visualisation commode de ce type d’opération modulaire peut se faire à l’aide d’un cadran d’horloge : 7h + 8h = 15h = 3h.

Le modèle utilisé pour apprendre cette opération est un Transformer, familier pour les tâches de NLP, dans lequel les chiffres sont interprétés comme des mots (ou des tokens) et sont donc représentés par des embeddings appris par le modèle à l’entraînement. Ce qui a surpris les chercheurs c’est que la structure des embeddings qui émergent après le grokking facilite ces opérations modulaires. Pour dire les choses simplement : ces embedding s’organisent spontanément selon des cadrans d’horloge adaptés à la valeur de p. La figure 11 illustre par exemple la position que prennent les embeddings des 28 entiers compris entre 0 et 27 dans un sous-espace qui facilite le calcul de l’addition du nombre 13 mod 28. Comme on le voit, cette opération se ramène en effet à un simple décalage angulaire sur le cadran. Chaque addition correspond en fait à un cadran dans un sous-espace dédié (non représenté ici).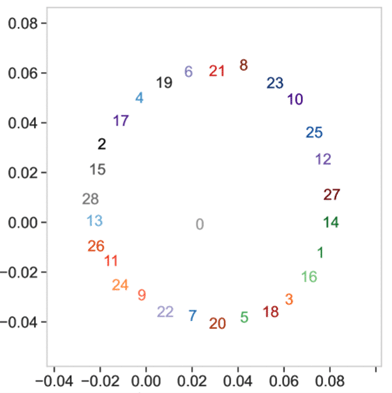

Figure 10 : agencement des embeddings des chiffres de 0 à 27 pour l’addition modulaire avec p=28 dans un sous-espace de l’espace de représentation des nombres qui représente l’addition mod 28 du nombre 13.

 

On retrouve donc un phénomène d’auto-organisation similaire à celui que nous évoquions pour l’encodage sémantique des mots. Il est par ailleurs associé à une transition de phase dans laquelle les embeddings des différents nombres se « cristallisent » selon un agencement qui facilite la solution du problème. Le modèle semble avoir réellement compris la structure du problème !

Se pourrait-il qu’un phénomène similaire soit à l’œuvre dans les LLM et que ceux-ci, à force d’apprentissage, finissent par comprendre progressivement des facettes du monde pour lesquelles ils construiraient des représentations internes ? Qu’un phénomène de grokking soit à l’origine des propriétés émergentes évoquées précédemment ? Là encore il s’agit de simples hypothèses.

La science en marche

Revenons à notre question initiale. Les LLMs comprennent-ils ce qu’ils écrivent ? Pour tenter de répondre à cette question il convient d’éviter deux écueils.

Le premier, le plus évident, est de céder à cet anthropomorphisme naïf qui nous incline à prêter aux LLM des facultés qu’ils n’ont pas. Il est tentant en effet de surinterpréter leur éloquence et leur assurance apparente comme une forme d’intelligence comparable à la nôtre. L’incongruité de certaines réponses, on l’a vu, doit cependant nous interpeler et nous inciter à la vigilance.

À l’inverse, à trop vouloir se prémunir de toute surinterprétation on peut développer une méfiance excessive sur les capacités réelles des LLM qui est en définitive aussi irrationnelle et stérile que l’excès de crédulité. Une attitude plus féconde serait de reconnaître que dans ces LLM pourvus de milliers de milliards de paramètres, et d’une complexité sans précédent, il se passe quelque chose de nouveau, quelque chose d’inattendu, quelque chose d’intéressant qu’on ne comprend pas et qui mérite d’être étudié avec toute la rigueur que requiert une investigation scientifique.

La science est fille de l’étonnement. Prétendre à l’esprit scientifique
tout en refusant l’étonnement devant l’imprévu est un oxymore.

Peut-être même peut-on déceler dans la posture des champions du scepticisme qui affirment « à moi, on ne la fait pas si facilement ! » une fierté mal placée. La fierté d’une espèce trop habituée à se concevoir comme seule dépositrice de l’intelligence authentique. Mais peut-on croire sérieusement qu’il n’existe qu’une seule forme d’intelligence et que ce soit précisément la nôtre ?

Sur la question de savoir ce que comprennent les LLM il n’existe aujourd’hui aucun consensus dans la communauté scientifique. Est-ce une surprise ? Non, car c’est ainsi que fonctionne la science. L’imprévu génère des interprétations différentes, des théories contradictoires, des polémiques parfois, jusqu’à ce qu’émerge un consensus à partir d’un dialogue où l’expérience et la théorie s’enrichissent mutuellement.

On aurait tort par conséquent d’accorder trop de crédit à toute position tranchée sur ces questions. Qu’elle émane de ceux qui ne voient dans les LLM que de vulgaires perroquets stochastiques ou, à l’inverse, qu’elle soit le fait des croyants en l’avènement imminent de la singularité technologique. Ces postures relèvent davantage d’une pensée qui cède au dogmatisme et au narcissisme que d’une perspicacité hors norme. Surtout, elles méconnaissent l’un des principaux ferments de la démarche scientifique qui est la fécondité du doute.

Références

1. Shalev-Shwartz, Shai, and Shai Ben-David. Understanding machine learning: From theory to algorithms. PDF. Cambridge university press, (2014).
2. Bubeck, Sébastien, et al. « Sparks of artificial general intelligence: Early experiments with GPT-4. » arXiv preprint arXiv:2303.12712 (2023).
3. Stéphane Mallat, La science des données – leçon inaugurale au collège de France (2018).
4. Power, Alethea, et al. « Grokking: Generalization beyond overfitting on small algorithmic datasets. » arXiv preprint arXiv:2201.02177 (2022).
5. David Louapre, Grokking: les modèles d’IA sont-ils capables de piger ?, blog Science Étonnante.
6. Schaeffer, Rylan, Brando Miranda, and Sanmi Koyejo. « Are emergent abilities of large language models a mirage? » Advances in Neural Information Processing Systems 36 (2024).
7. Guo, Siyuan, et al. « Learning Beyond Pattern Matching? Assaying Mathematical Understanding in LLMs. » arXiv preprint arXiv:2405.15485 (2024).
8. Kaplan, Jared, et al. « Scaling laws for neural language models. » arXiv preprint arXiv:2001.08361 (2020).
9. Arora, Sanjeev, and Anirudh Goyal. « A theory for emergence of complex skills in language models. » arXiv preprint arXiv:2307.15936 (2023).
10. Mikolov, Tomáš, Wen-tau Yih, and Geoffrey Zweig. « Linguistic regularities in continuous space word representations. » Proceedings of the 2013 conference of the north american chapter of the association for computational linguistics: Human language technologies. 2013.

 

^1. On pourrait rapprocher les LLM des objets mystérieux décrits dans le célèbre roman Stalker des frères Strougatski. Abandonnés par une civilisation extraterrestre, personne ne comprend réellement le fonctionnement de ces artefacts mais ceci n’empêche nullement de les utiliser pour faire du profit !
^2. Des lois d’échelles empiriques ont été établies à cet effet [8].
^3. Étant incapable d’agir sur le monde, ils n’ont pas d’expérience causale directe ce qui limite leur capacité à anticiper les effets de certaines actions.
^4. Par analogie avec la matière noire de nature inconnue dont les physiciens spéculent l’existence pour rendre compte du mouvement de rotation des galaxies.
^5. Ce sont des lois de puissance caractérisées par des exposants critiques.