La causalité et l’IA : une histoire de cigognes

1.   Une histoire de cigognes

Tout le monde connaît cette vieille légende d’Europe centrale qui raconte comment les cigognes apportent les bébés, enveloppés dans un linge, pour les livrer aux parents par la cheminée. L’origine de cette légende, qui remonte au XIXᵉ siècle, est probablement à chercher dans un socle culturel associant les cigognes à la fertilité et au renouveau. Ces oiseaux reviennent effectivement sous nos latitudes au printemps pour nicher sur les cheminées des habitations rurales. Il n’est pas invraisemblable qu’un habitat prospère, ainsi que différents facteurs sociologiques favorisant les relations sociales neuf mois avant l’arrivée du printemps, puissent expliquer rationnellement une coïncidence réelle à l’origine de ce conte pour enfants.

À condition de disposer de données démographiques et économiques en quantité et en qualité suffisantes, on pourrait entraîner un modèle de machine learning afin de prédire un taux de natalité saisonnier en fonction d’un certain type d’habitat. Entraîné sur les données de l’Alsace rurale du XIXᵉ siècle, un tel modèle ferait sans doute des prédictions plus précises que le simple hasard. Mais, que le réchauffement climatique incite les cigognes à choisir un autre lieu de villégiature ou que le chauffage électrique remplace les cheminées, et notre algorithme deviendrait soudainement obsolète !

Le seul mérite de cette petite mise en scène, on l’aura compris, est d’illustrer que l’absence de prise en compte des « vraies » relations causales par notre modèle le rend vulnérable aux changements affectant la distribution statistique des données. En termes techniques, on dit que l’algorithme ne généralise pas hors distribution (Out Of Distribution – OOD), car il n’exploite que des corrélations trompeuses, propres à une situation particulière, sans considération pour le mécanisme causal ayant généré les données.

Pour éviter de telles situations, on est contraint, en apprentissage automatique, de supposer que les données d’entraînement d’un modèle possèdent les mêmes propriétés statistiques que celles de l’environnement dans lequel il est censé faire des prédictions. On dit alors que les données des deux environnements sont indépendantes et identiquement distribuées (i.i.d.). Cependant, il ne s’agit que d’une hypothèse simplificatrice, dont l’unique vertu est de fournir un cadre mathématique permettant de garantir que l’algorithme produira des prédictions utiles. Hélas, cette hypothèse est souvent démentie par la pratique !

Un exemple extrême de la vulnérabilité induite par l’hypothèse i.i.d. lorsqu’elle n’est pas respectée est celui d’un classifieur d’images qu’un léger bruit artificiel, même imperceptible à l’œil humain, peut induire en erreur, lui faisant, par exemple, croire qu’une photo de perroquet représente un autobus ! Il n’y a là aucun mystère : n’ayant jamais vu d’image de perroquet bruitée, l’algorithme se trompe misérablement. Force est donc de constater que l’intelligence de ce type de modèle prédictif statistique reste extrêmement limitée.

L’intelligence animale et humaine, celle qui leur confère l’autonomie indispensable à leur survie dans des environnements physiques et sociaux complexes, est naturellement d’une tout autre nature.

 

Identifier des mécanismes causaux à partir d’observations et d’expériences passées pour en tirer parti dans des contextes variés est le vrai marqueur de l’intelligence animale et humaine.

 

Dans l’idéal, c’est ce type d’intelligence, à la fois causale et adaptative, que l’on souhaite reproduire avec l’IA. Se posent alors plusieurs questions fondamentales. Comment distinguer les relations causales des corrélations trompeuses dans un ensemble d’observations ? Et, avant cela, comment définir et formaliser le concept même de causalité, sachant qu’il n’a pas sa place dans les statistiques classiques ? La suite de cet article propose un survol de ces questions : certaines ont récemment bénéficié d’avancées significatives, tandis que d’autres restent l’objet de recherches en cours.

2. Des heuristiques pour identifier les relations causales

Quels indices révèlent l’existence d’une relation causale entre deux phénomènes ? Pour répondre à cette question délicate, de nombreuses règles heuristiques, plus ou moins plausibles et justifiées, ont été élaborées au fil des siècles par certains philosophes, par les physiciens bien sûr, et, plus récemment, par des statisticiens audacieux [1,2,3]. Nous en décrirons succinctement quatre dans cette section.

La formalisation de certaines de ces règles a conduit à la définition des modèles structurels causaux (SCM) et au principe de minimisation du risque invariant (IRM), que nous aborderons dans la section 3. Ces deux outils de modélisation permettent d’intégrer les questions causales dans le machine learning. Ils permettent, sous certaines conditions, des réponses aux deux questions fondamentales que sont l’identification des relations causales et la prédiction de l’effet d’une intervention sur un système.

La chronologie des évènements

Le premier élément qui vient à l’esprit lorsque l’on pense à une relation causale entre deux évènements est leur relation chronologique.

 

Une cause précède toujours ses conséquences.

 

C’est une condition nécessaire, mais elle n’est évidemment pas suffisante. Si l’arrivée des cigognes précède une naissance, elle n’en est pas pour autant la cause. Nous reviendrons sur la question de la chronologie dans la section suivante, où nous décrirons les différents niveaux de modélisation envisageables d’un système, ceux-ci se distinguant, entre autres, par leur prise en compte de la temporalité des événements.

Le principe de Reichenbach

 

Si l’on observe une corrélation entre deux phénomènes X et Y et que l’on peut exclure que l’un soit la cause de l’autre, alors on en peut en conclure qu’il existe une cause commune aux deux. C’est le principe de Reichenbach.

 

Lorsque la cause expliquant la corrélation n’est pas connue, on parle de facteur de confusion ou, plus souvent, de « confounder ».

Dans notre histoire, X pourrait représenter le nombre de cigognes venues nicher dans une région, Y le taux de natalité, et Z le mouvement du soleil autour de la Terre, qui influence à la fois les relations sociales et les migrations des oiseaux.

Le principe des causes indépendantes (ICM)

Lorsque nous examinons un objet, notre cortex visuel suppose que notre point de vue et l’objet qu’il analyse sont indépendants. Cette hypothèse est généralement utile, car elle est vérifiée dans l’immense majorité des cas. Lorsqu’elle est violée, nous percevons une illusion d’optique !

Il s’agit là d’une hypothèse qui illustre un principe plus général appelé le principe des causes indépendantes (ICM pour Independant Causal Mechanisms) [1,2] :

 

ICM stipule que les données d’observations sont le plus souvent générées par des mécanismes autonomes. Ils sont indépendants au sens où la connaissance d’un mécanisme ne nous informe en rien sur un autre.

 

Considérons un autre exemple où l’on s’intéresse à la relation entre la température de l’air T et l’altitude A à laquelle cette température est mesurée. Imaginons que les couples (A,T) soient relevés dans différentes localités des Alpes et des Vosges. Les distributions p(A) des altitudes varieront naturellement d’un massif à l’autre. Les distributions conditionnelles p(T∣A), causales car déterminées par les lois de la physique, seront en revanche identiques. Autrement dit, une intervention sur l’altitude A modifiera p(A) sans affecter la relation causale p(T∣A).

La règle de Bayes nous permet d’exprimer la distribution conjointe des deux variables comme le produit des facteurs associés à chaque mécanisme : p(A,T) = p(A) p(T∣A). La statistique des observations variera donc d’un massif à l’autre, puisque pAlpes(A) ≠ pVosges(A). En revanche, la distribution conditionnelle p(T∣A), qui décrit un mécanisme causal, demeure quant à elle invariante.

La conclusion que nous souhaitons tirer de ces remarques est que l’identification d’invariances dans la description d’un système, le facteur p(T∣A) dans notre exemple, constitue une piste sérieuse pour déceler des relations causales et pour construire des modèles prédictifs capables de faire des prédictions OOD.

Le principe du « Sparse Mechanism Shift » (SMS)

Ce dernier principe peut se concevoir comme une conséquence du précédent.

Remarquons que rien ne nous empêche de factoriser la distribution conjointe de l’exemple précédent de manière non-causale, à savoir selon p(A,T) = p(T) p(A|T). Le point intéressant à noter est qu’une intervention sur l’altitude A se manifeste cette fois simultanément sur les deux facteurs. D’une part sur p(T), car T est impacté par A via la relation causale, et, d’autre part, sur la distribution conditionnelle p(A|T) puisqu’on intervient directement sur A. Le principe SMS généralise cette observation :

 

Dans le monde physique, les interventions sur un système se manifestent par la modification d’un petit nombre de facteurs dans la factorisation causale de la distribution des observations.

 

A l’inverse, lorsque la factorisation n’est pas causale, une intervention aura en général un impact sur tous les facteurs comme l’illustre notre exemple.

3. Les statistiques ne suffisent pas !

L’échelle de causalité

Judea Pearl, informaticien et philosophe américain, lauréat du prix Turing en 2011 et inventeur d’une approche des problèmes de causalité, a proposé une représentation symbolique des différents types de prédictions utiles en pratique. Celle-ci est désignée sous le nom d’échelle de la causalité.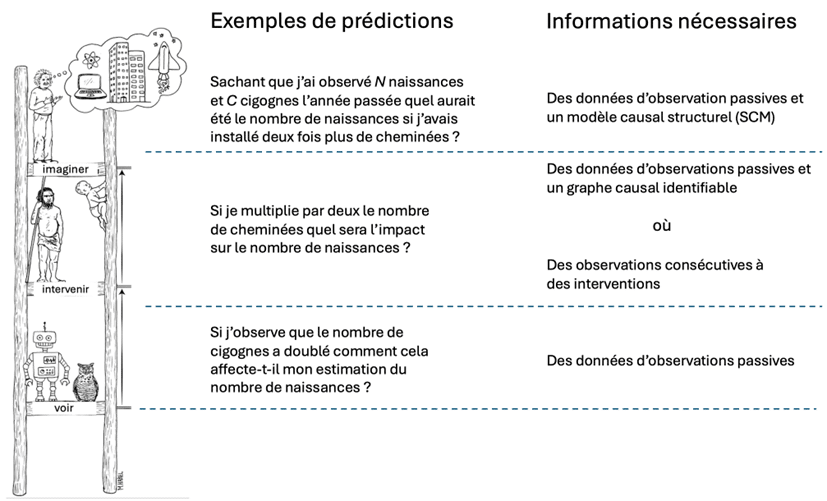

L’échelon « voir »

Au premier échelon, on trouve les questions auxquelles le machine learning, dans sa version usuelle, peut répondre. Il s’agit ici d’établir des corrélations du type : si j’observe l’événement A (arrivée de nombreuses cigognes), comment cela affecte-t-il ma croyance concernant l’observation de l’événement B (nombre de naissances) ? Aucune causalité ici ; on se contente d’élaborer un modèle statistique prédictif qui exploite les corrélations entre les deux événements A et B, établies à partir d’un historique.

L’échelon « intervenir »

Au second échelon, on trouve les questions portant sur l’effet d’une intervention sur un système. Il ne s’agit pas seulement d’observer le monde, mais d’agir sur lui. Les statistiques, dans leur formulation traditionnelle, ne sont pas en mesure de répondre à ce type de question. Pearl et d’autres chercheurs ont cependant montré que, dans certaines situations favorables, il est possible d’y répondre, à condition de disposer à la fois de données en quantité suffisante et d’un graphe des relations causales.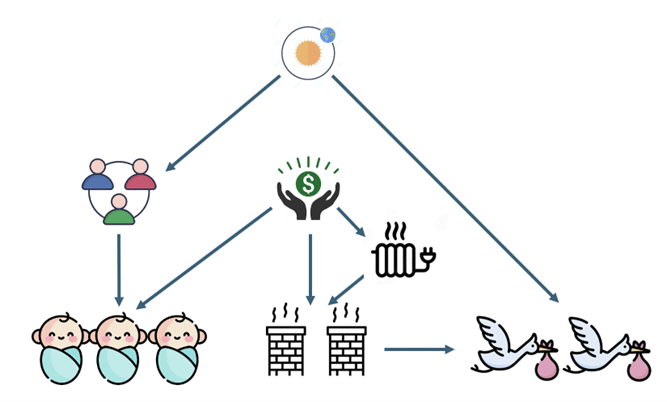

Graphe (hypothétique) des relations causales qui pourrait « expliquer » l’origine du conte des cigognes. La marche du soleil impacte les relations sociales et les migrations. La prospérité d’une région et la disponibilité d’un chauffage électrique déterminent le nombre de chaumières dotées de cheminées propices à accueillir des cigognes, etc.

Insistons sur le fait que cette identification n’est pas toujours possible. Elle requiert en effet que le graphe causal satisfasse certaines conditions dites d‘identifiabilité [1,3]. Certaines d’entre elles s’expriment sous forme de règles graphiques, la plus connue étant la règle de la porte arrière (backdoor rule). Dans des situations complexes, ces conditions sont plus facilement exprimées à l’aide de règles algébriques, qui constituent ce qu’on appelle le do-calculus. Le point principal à retenir est le suivant.

 

En l’absence d’informations sur la structure causale du mécanisme de génération des données, il est impossible d’identifier les relations de causalité à partir d’observations passives. Si le graphe causal est connu et vérifie certaines conditions, l’identification devient alors possible.

 

Un graphe causal peut être conçu comme la formalisation, par un expert d’un domaine (agronome, biologiste, économiste…), des relations causales reliant les différentes variables intervenant dans un problème relevant de son champ de compétence

Une autre approche, sans doute plus intuitive, pour identifier ces relations consiste à soumettre le système à un ensemble varié d’interventions, puis à observer leur impact sur ses différentes variables.

L’échelon « imaginer »

Le dernier échelon, enfin, est celui de l’imagination. Il regroupe les questions contrefactuelles concernant des situations hypothétiques. Reprenons une fois encore notre exemple fil rouge pour illustrer notre propos. On cherche ici à répondre à des questions du type :

« Sachant qu’on a observé N naissances lorsque C cigognes sont arrivées au printemps, combien aurait-on observé de naissances si l’on avait doublé le nombre de rencontres à la fin de l’été et triplé le nombre de cheminées ? »

Pour répondre à ce type de questions, on peut montrer [1,3] que même la connaissance du graphe causal en plus des données ne suffit pas. Il faut avoir accès à ce qu’on appelle le modèle causal structurel (SCM, pour Structural Causal Model). Sans entrer dans les détails, un tel modèle spécifie de manière quantitative comment chaque variable dépend de ses causes directes, cette relation étant le plus souvent bruitée par des causes que l’on renonce à décrire.

Dans l’exemple des cigognes, un SCM spécifierait, par exemple, comment le nombre de cigognes dépend de la saison et du nombre de cheminées disponibles. Chaque SCM détermine naturellement, de manière univoque, un graphe causal.

Les modèles causaux décrits par des SCM n’intègrent aucune variable temporelle. Ils décrivent les dépendances fonctionnelles qui caractérisent comment chaque variable réagit à toutes les interventions possibles sur les autres variables. On peut en fait concevoir les SCM comme une synthèse formelle des heuristiques évoquées dans la section 2. Une rapide comparaison avec les modélisations proposées respectivement par la physique et la statistique permettra d’éclairer davantage la nature des SCM.

En physique, on modélise traditionnellement l’évolution temporelle d’un système à l’aide d’équations différentielles. Celles-ci ont été élaborées au cours des siècles par les physiciens, qui ont ainsi codifié un grand nombre de résultats expérimentaux. Ces modèles permettent de prédire comment un système évolue à partir d’une condition initiale et, par conséquent, d’anticiper l’impact d’une intervention sur ces conditions.

À l’inverse, une modélisation statistique ne requiert aucune expertise pour formuler un modèle. Elle se contente d’établir des corrélations entre des observations, cette frugalité conceptuelle étant précisément ce qui fait sa force.

Les SCM se situent entre ces deux extrêmes : ils partent des données, mais remplacent l’expertise du physicien par une description ad hoc et atemporelle des dépendances fonctionnelles entre causes et effets [2].

Pour conclure ce long développement sur l’échelle de la causalité, précisons que l’inférence causale est une branche des mathématiques appliquées qui s’attache à répondre à de nombreuses questions analogues à celles que nous venons d’esquisser. Par exemple :

  • « Que peut-on dire d’un graphe causal si l’on ne dispose que d’observations passives ? »
  • « Quelles interventions sont nécessaires pour déterminer à moindre coût toutes les relations causales ? »
  • « Quelles prédictions peut-on faire pour un système dont le SCM n’est pas connu avec certitude ? »

etc. [1,3].

Les difficultés avec les données perceptuelles

Les SCM présupposent que l’on sache identifier et décrire le rôle de chaque variable d’un système. C’était notamment le cas dans l’exemple du fil rouge, et cela vaut également pour d’innombrables modèles prédictifs élaborés par des experts en économie, en pharmacologie, en chimie, en biologie, etc.

Cependant, dans beaucoup de situations, cette hypothèse ne tient pas. Les applications de l’IA basées sur le deep learning reposent aujourd’hui sur des données non structurées, telles que des images, des sons ou du texte. Appelons-les globalement des données perceptuelles. Ces données sont encodées sous forme de représentations distribuées, c’est-à-dire des vecteurs (embeddings) de grande dimension, dont les composantes n’ont aucune interprétation causale directe.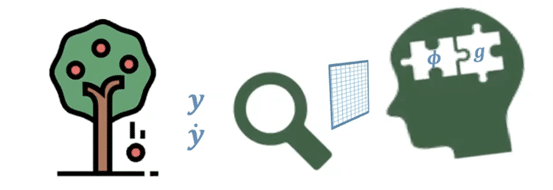

Extraction de représentations invariantes à partir de données perceptuelles. Φ symbolise l’extraction et g est un prédicteur qui utilise ces représentations.

 

Une simple image mentale peut aider à saisir la difficulté de faire des prédictions robustes à partir de données perceptuelles. Imaginons une pomme tombant d’une branche et supposons que nous nous intéressions à la relation causale entre sa position et son mouvement, considérés comme des causes, et la vitesse avec laquelle elle percute le sol, vue comme une conséquence. Imaginons en outre que Newton n’ait pas encore découvert l’équation qui lui a valu la postérité, mais que nous disposions néanmoins de milliers d’enregistrements de chutes de pommes, observées dans des conditions variées.

Pour résoudre notre problème de prédiction, il nous faudra identifier les variables causales que sont la position et la vitesse initiale de la pomme à partir de données brutes constituées de milliards de pixels (ou des embeddings des vidéos). Ce qui nous permettra d’identifier ces causes en pratique, c’est leur invariance : elles ne dépendent ni de l’arbre, ni de la couleur de la pomme, ni des conditions de prise de vue du film. Ce travail d’identification et d’extraction des causes à partir des données perceptuelles n’est ni plus ni moins que l’élaboration d’une théorie. C’est précisément ce qu’a accompli Newton ! À ce jour, aucune IA n’est capable d’une telle prouesse, et ce processus cognitif d’induction d’une théorie à partir de l’observation conserve une large part de mystère.

L’objectif de cette petite mise en scène est de faire comprendre que :

 

La clé pour découvrir des relations causales à partir de données perceptuelles est d’extraire des représentations invariantes à partir d’une variété suffisante d’environnements.

 

Plusieurs travaux de recherche récents [4,5] partent de cette idée pour essayer d’élaborer des méthodes de prédictions robustes aux changements de domaine (OOD). La méthode dite de minimisation du risque invariant (IRM) [5] a en particulier reçu une grande attention même si elle est encore loin d’avoir résolu tous les problèmes. Elle se fixe pour objectif de construire des classifieurs, d’images ou de textes, qui apprennent à extraire des features qui demeurent prédictives d’un environnement à un autre. En d’autres termes, IRM apprend à négliger les corrélations trompeuses, qui ne sont présentes que dans certains environnements et ne peuvent donc être le support d’une généralisation plus large.

Un travail récent en TAL (Traitement Automatique du Langage) [6] applique les idées d’IRM avec l’objectif de construire des LLM que l’on peut entraîner sans risques de biais à partir d’environnement aussi varié que des articles Wikipédia, des réseaux sociaux, des articles de presse, des évaluations de produits et de services etc…

4.   L’impact de la causalité sur le machine learning

Donnons quelques exemples où la prise en compte de considérations causales permet soit d’améliorer certaines prédictions faites par le machine learning, soit d’apporter un nouvel éclairage sur des techniques existantes. Cette section, inspirée de la section VII de l’article [2], s’adresse en priorité aux data scientists.

Le ML semi-supervisé

Dans une approche probabiliste, entraîner un classifieur à prédire une cible Y à partir de features X revient à estimer la probabilité conditionnelle P(Y∣X). Le ML semi-supervisé (SSL) repose sur l’idée, ou l’espoir, que la distribution P(X) des features contient une information, généralement négligée, qui peut améliorer l’estimation de P(Y∣X). Par exemple, l’hypothèse de clustering suppose que chaque cluster de P(X) correspond à une valeur distincte de la cible Y.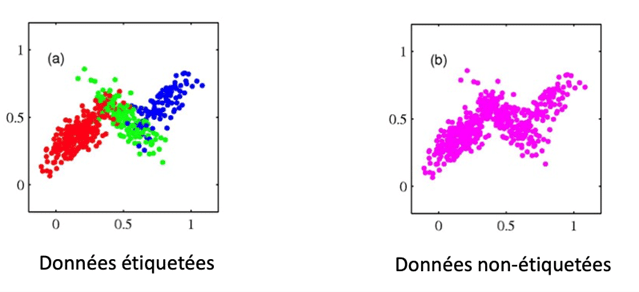

Supposons que les features X soient la cause de la cible Y que l’on cherche à prédire. Dans ce cas, le principe ICM nous dit que la distribution P(X) des causes est indépendante du mécanisme causal décrit par P(Y∣X), une conclusion qui entre en contradiction directe avec l’hypothèse du SSL !

En revanche, si l’on se place dans un contexte anti-causal où la cible Y est la cause des features prédictives X, alors cette contradiction disparaît.

 

L’apprentissage semi-supervisé d’une relation entre des features X et une cible Y n’est cohérent que dans le cas anti-causal.

 

La robustesse aux attaques adversariales

La causalité joue également un rôle dans la robustesse de certains prédicteurs vis-à-vis des attaques adversariales. Les classifieurs d’images basés sur les réseaux de neurones de convolution y sont particulièrement vulnérables, un simple bruit, même imperceptible pour un humain, peut en effet les induire à faire des prédictions fantaisistes. Ceci n’est guère surprenant lorsque l’on réalise que l’hypothèse i.i.d. est clairement violée dans un tel contexte : les perturbations artificielles ont en effet une distribution radicalement différente de celle des données non perturbées correspondant aux images naturelles.

Imaginons que le modèle génératif d’une collection d’images soit anti-causal, c’est-à-dire que les images X soient générées à partir d’un label Y descriptif. Le principe ICM nous suggère alors que les distributions P(Y) et P(X∣Y) sont indépendantes l’une de l’autre. Une intervention sur Y aura un impact sur l’image X, mais une intervention sur X n’aura aucun effet sur Y. Ceci suggère qu’il est plus judicieux d’apprendre le modèle génératif P(X∣Y) plutôt que P(Y∣X) qui est instable face aux petites perturbations de l’image X.

La distribution recherchée P(Y∣X) pour une image X donnée s’obtient par la formule de Bayes P(Y|X) = const P(X|Y) P(Y). Le second facteur est facile à estimer puisqu’il correspond à la proportion des différentes classes d’images dans l’ensemble d’entraînement. Cette approche par modèle génératif a permis d’établir un nouvel état de l’art en termes de robustesse pour un classifieur d’images [7].

Les décisions stratégiques

Considérons un modèle de machine learning conçu pour prédire le risque de non-remboursement d’un crédit par un emprunteur dont on connaît le taux d’endettement et le lieu de résidence.

Pour accroître ses chances d’obtenir le prêt qu’il convoite, l’emprunteur pourra jouer sur ces deux facteurs. Il peut choisir de rembourser une partie de ses dettes ou opter pour un déménagement dans un secteur mieux noté par son assureur. La première option aura évidemment un impact sur sa solvabilité, tandis que la seconde n’en aura aucun. Pour se prémunir de ce type de stratagème, un assureur pourrait donc avoir intérêt à utiliser un modèle prédictif qui n’utilise que des variables causales. Son modèle pourrait perdre en prédictivité ce qu’il gagne en robustesse, et ce choix devra donc être éclairé.

La data augmentation

La technique de data augmentation consiste à augmenter la diversité d’un jeu de données d’entraînement au moyen d’observations artificielles générées dans l’objectif d’apprendre certaines invariances à un modèle de ML, afin de favoriser la prise en compte d’informations causales.

Imaginons que nous souhaitions entraîner un modèle qui associe une profession à une lettre de motivation, sans que le genre ou l’origine du candidat n’ait d’impact. Pour favoriser l’émergence d’un classifieur équitable, on pourrait procéder à un enrichissement des données d’entraînement à l’aide d’observations fictives, appelées contrefactuels. Celles-ci correspondent à des observations dans lesquelles on a modifié le genre ou l’origine, toutes choses égales par ailleurs, afin d’équilibrer le jeu de données [8].

De même, on pourra enrichir le jeu de données d’un classifieur d’images à l’aide d’images prises sous différents angles de vue pour entraîner le modèle à ignorer cette information qui n’a pas de contenu sémantique.

L’apprentissage par renforcement

L’objectif de l’apprentissage par renforcement (RL) est de concevoir des agents autonomes capables de prendre des décisions et d’agir sur leur environnement afin de maximiser un gain à long terme. Plus précisément, on cherche à élaborer une stratégie optimale qui associe à chaque état de l’environnement une action de l’agent. Le rapprochement avec le domaine de la causalité est donc immédiat, car un tel agent ne se contente pas d’observer son environnement, mais agit sur lui, ce dernier l’informant en retour de l’efficacité ponctuelle de chaque action. Un agent de ce type se situe donc d’emblée à l’échelon n°2 de l’échelle de causalité.

On distingue deux champs de recherche à l’intersection de la causalité et du RL. Le premier est l’induction causale, qui consiste à faire découvrir la structure causale de l’environnement par un agent intervenant sur celui-ci. Le second est l’inférence causale, qui vise à exploiter un modèle causal de l’environnement pour choisir une succession d’actions optimales.

5.   Penser c’est agir dans un monde imaginaire !

La prise en compte de la causalité permet, comme nous l’avons vu, de surmonter certaines limitations du machine learning (ML) dans sa forme usuelle. L’hypothèse i.i.d. limite en effet sévèrement les capacités de généralisation de ces modèles classiques, qui ne pourront jamais acquérir qu’une compréhension superficielle et statique du monde.

L’intégration de la causalité aux modèles prédictifs paraît incontournable pour concevoir des modèles capables de raisonner, de planifier et d’intervenir sur leur environnement afin d’y recueillir les données utiles à la réalisation d’un objectif dans des environnements physiques ou sociaux complexes [2]. La route pour y parvenir est certes encore longue et de nombreux problèmes demeurent ouverts, au premier rang desquels l’identification de ces abstractions que sont les variables causales interprétables à partir de données perceptuelles.

 

Cependant, parvenir à intégrer étroitement la causalité dans le ML rapprocherait l’IA de la conception de l’intelligence formulée par le célèbre éthologue Konrad Lorenz, qui concevait la pensée comme une action dans un univers imaginaire.

 

Si la chose était possible, certains chercheurs [2] considèrent qu’il serait même possible de définir l’émergence d’une conscience chez un agent comme la représentation qu’un agent construit de lui-même dans le monde imaginaire où agit sa pensée. De même, le libre arbitre de cet agent pourrait alors être assimilé à un moyen, pour un tel agent doté de conscience, de communiquer avec le monde extérieur pour expliquer ses décisions.

Quelle que soit la validité de ces spéculations un peu audacieuses, une chose est sûre : la causalité est loin d’avoir dit son dernier mot dans les avancées de l’IA.

Références

  1. Peters, J., Janzing, D., & Schölkopf, B. (2017). Elements of causal inference: foundations and learning algorithms (p. 288). The MIT Press.
  2. Schölkopf, B., Locatello, F., Bauer, S., Ke, N. R., Kalchbrenner, N., Goyal, A., & Bengio, Y. (2021). Towards causal representation learning. Proceedings of the IEEE, 109(5), 612-634.
  3. Pearl, J. (2009). Causality. Cambridge university press.
  4. Peters, J., Bühlmann P., Meinshausen N. (2015). Causal Inference using Invariant Prediction. arXiv preprint arXiv:1501.01332.
  5. Arjovsky, M., Bottou, L., Gulrajani, I., & Lopez-Paz, D. (2019). Invariant risk minimization. arXiv preprint arXiv:1907.02893.
  6. Peyrard, M., Ghotra, S. S., Josifoski, M., Agarwal, V., Patra, B., Carignan, D., … & West, R. (2021). Invariant language modeling. arXiv preprint arXiv:2110.08413.
  7. Schott, L., Rauber, J., Brendel, W., & Bethge, M. (2018). Towards the first adversarially robust neural network model on MNIST. 2019. URL https://arxiv. org/pdf/1805.09190. pdf.
  8. Lemberger, P., & Saillenfest, A. (2024). Explaining Text Classifiers with Counterfactual Representations. arXiv preprint arXiv:2402.00711.

Auteur

Ces contenus peuvent vous intéresser…